CONJUNTOS
INTRODUCCION
En este capítulo se estudian los conceptos básicos de la
teoría intuitiva de conjuntos, notaciones, subconjuntos, sus operaciones y sus
aplicaciones. Para alcanzar los fines prácticos que nos interesan se completa
con bastante cantidad de ejemplos ilustrativos
El desarrollo histórico de la teoría de conjuntos se
atribuye a Georg Cantor, que comenzó a investigar cuestiones conjuntistas
(puras) del infinito en la segunda mitad del siglo XIX, precedido por algunas
ideas de Bernhard Bolzano e influido por Richard Dedekind.
CONCEPTO Y NOTACIÓN DE CONJUNTO
En el lenguaje corriente, empleamos el vocablo conjunto
para referirnos a una pluralidad o colectividad de objetos que se consideran
agrupados formando un todo. Por ejemplo, conjunto de alumnos de una clase;
conjunto de letras del abecedario; conjunto de escritores nacionales, etc. De
esta noción de pluralidad contrapuesta a la de singularidad ha surgido el
concepto matemático de conjunto. Los ejemplos recién mencionados bastan por
ahora para tener una idea de dicho concepto. Lo esencial de dichas situaciones
es la presencia de elementos o miembros del conjunto, los mismos se les denota
usualmente por letras minúsculas como a, b, c,..., y los conjuntos se denotan
por lo común mediante letras mayúsculas como A, B, C, .... Otros símbolos de
uso frecuente son:

Como acabas de ver, es posible representar gráficamente los
conjuntos a través de diagramas de Venn. Para trabajar con ellos es
necesario poder representarlos también con el lenguaje propio de la matemática.
Se usan los corchetes para representar y definir conjuntos. En el
interior de los corchetes se ubican los elementos que conforman el conjunto
separado por comas. Esta representación escrita es equivalente a la
representación gráfica de diagramas de Venn.
Si por ejemplo se quiere definir el conjunto como el
conformado por los elementos , , , y se puede
representar de las siguientes formas
Descripción de
conjuntos por extensión
Para describir los elementos de un determinado conjunto los puedes mencionar uno a uno, a esto se conoce como descripción por extensión. Definamos como el conjunto conformado por los colores del arco iris, en este caso podemos describir el conjunto por extensión así:
Si un conjunto tiene muchos elementos puedes hacer uso de
los puntos suspensivos para describir el conjunto por extensión. Por
ejemplo, si el conjunto está conformado por los cien primeros números
enteros, puedes representarlo de la siguiente manera:
En este caso no se muestran los cien elementos que conforman
el conjunto. Sin embargo, los puntos suspensivos representan todos los
elementos que, por comodidad, no hemos escrito.
Descripción de
conjuntos por comprensión
En algunos casos los conjuntos pueden tener una variada
cantidad de elementos y la descripción por extensión resultaría muy ardua. Se
puede entonces describir los conjuntos mencionando las características que comparten
los elementos que los conforman. Por ejemplo, si es el conjunto
conformado por todos los países del mundo se puede escribir:
En donde la barra | se lee como “tales que”.
Así, la anterior expresión se lee: “ es el conjunto de
los tales que es un país”. En este caso el símbolo
es usado simplemente para representar los elementos del conjunto .
Clases de conjuntos
Existen varios tipos de conjuntos que se destacan por sus
características especiales. Conocerlos te ayudará a comprender mejor la
estructura y el mundo de los conjuntos
Conjunto Universal
Con el ánimo de evitar confusiones, cuando definimos un
conjunto debemos especificar de dónde se están tomando los elementos que lo
conforman. Esto significa que debe existir una base de la cual tomamos
estos elementos, esta base sobre el cual trabajamos es llamada conjunto
universal. Usaremos siempre la letra para representar el
conjunto universal.
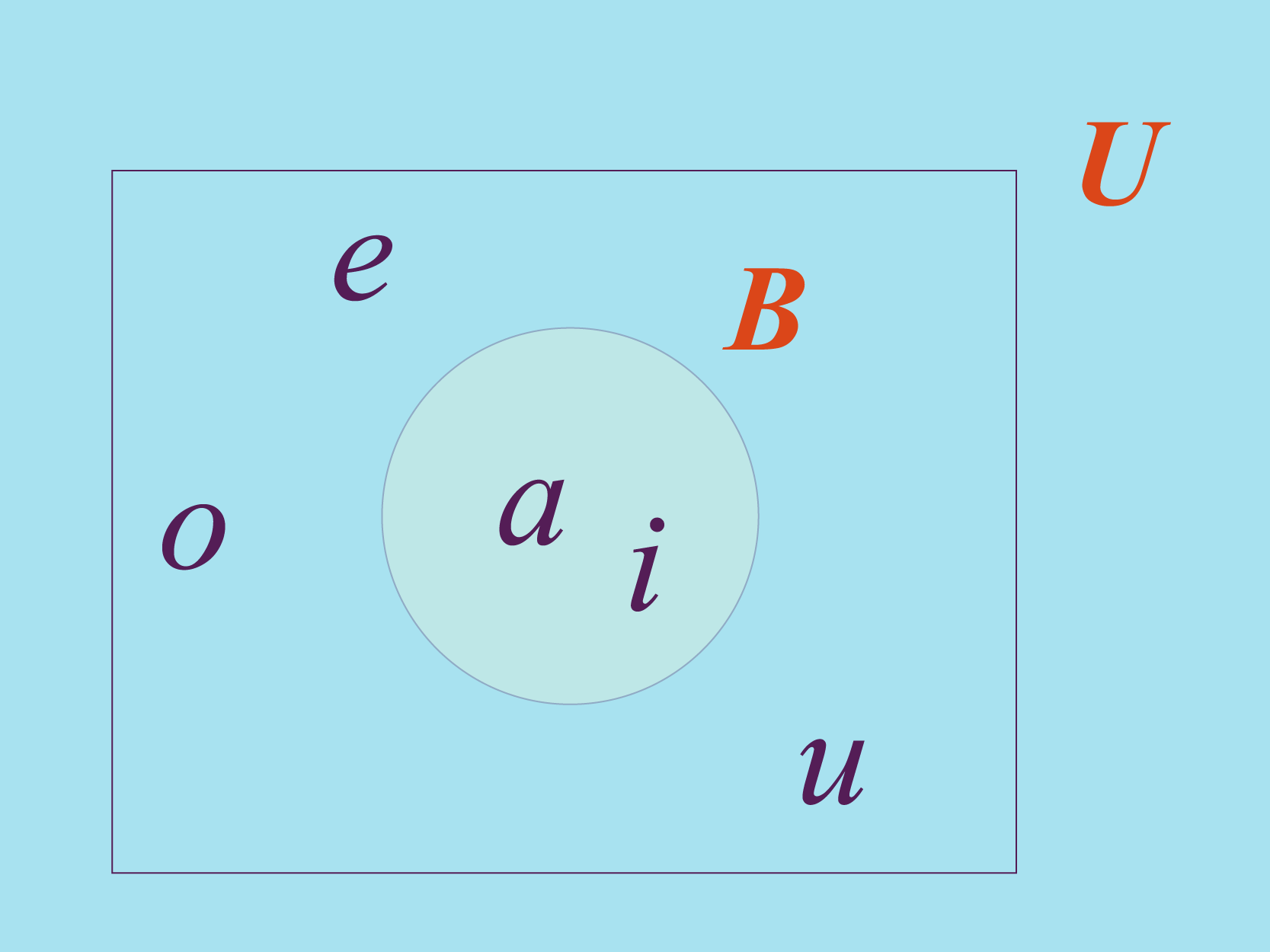
Por ejemplo, si quieres definir B como el
conjunto conformado por las vocales A e I, el conjunto
universal podría ser el conjunto de las vocales. En la figura anterior se
muestra cómo puedes usar los diagramas de Venn para representar la relación
entre el conjunto B y su conjunto universal U .
Observa que el conjunto universal puede tener exactamente
los elementos de los conjuntos que abarca o más.
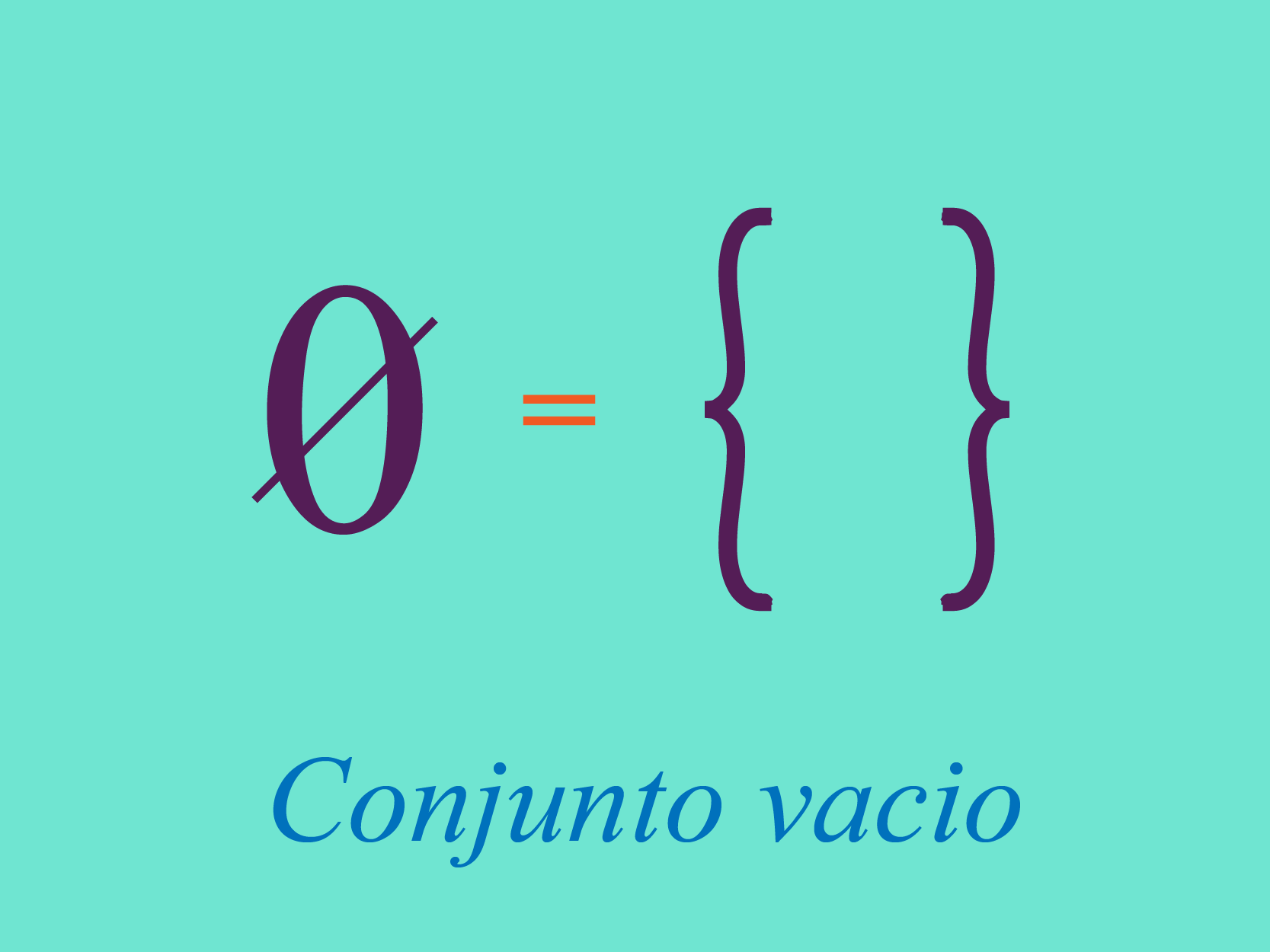
Conjunto vacío
Consideremos la existencia de un conjunto que no tiene
elementos, este es llamado conjunto vacío. Para representar
dicho conjunto usamos el reconocido símbolo del vacío, como se muestra en la
imagen de abajo:
También, haciendo uso de la descripción
por extensión, representamos el conjunto vacío por medio de los
corchetes {} . Como el conjunto vacío no tiene elementos, no podemos
ubicar ningún elemento en el interior de los corchetes.
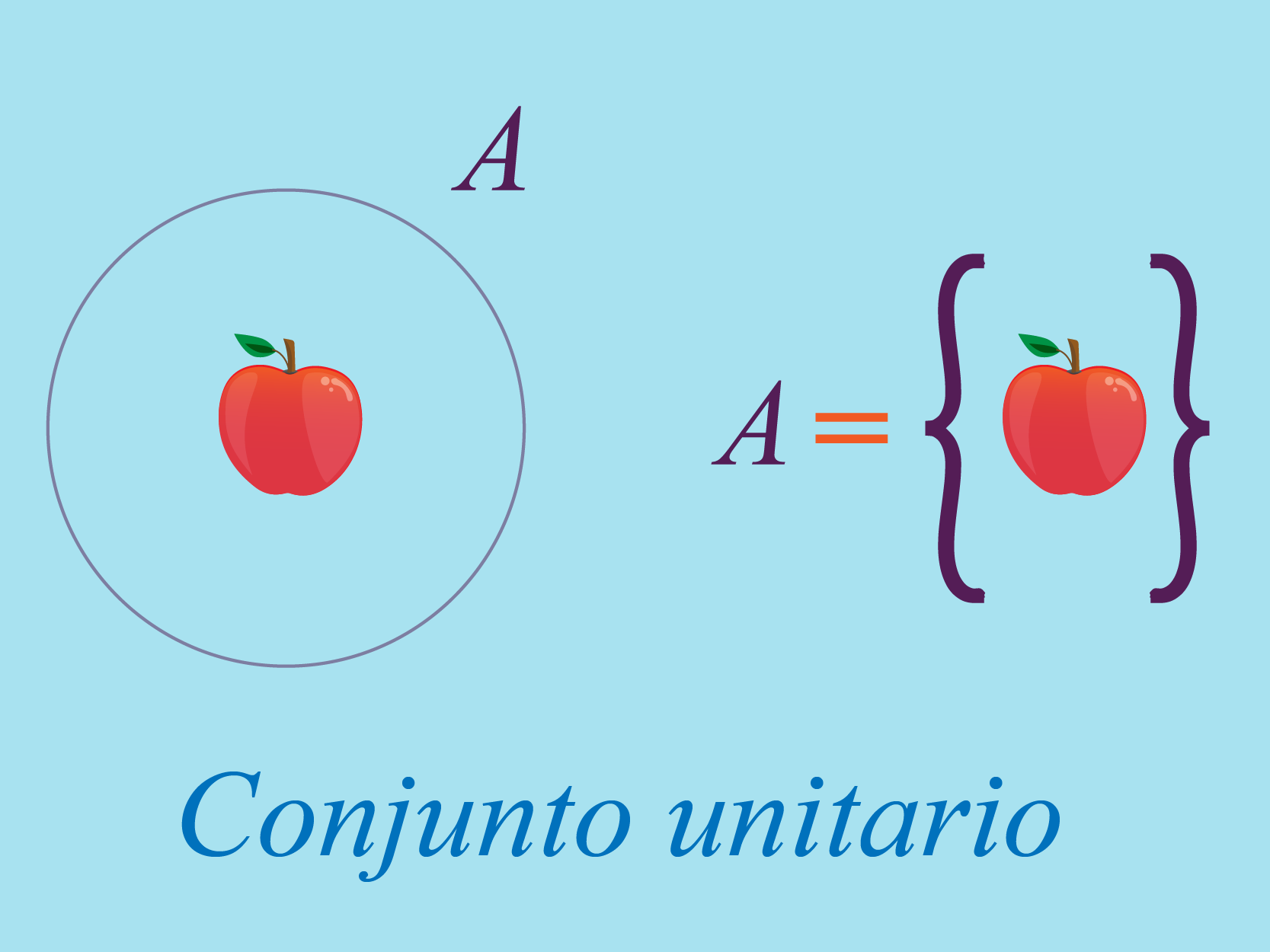
Conjuntos unitarios
El conjunto unitario se distingue por tener solo
un elemento. No importa qué tipo de elemento tenga el conjunto, un gato,
un perro, un número, una letra o cualquier otra cosa, si tiene un solo elemento
es llamado conjunto unitario.
Conjuntos finitos
Este tipo de conjunto también se distingue por la cantidad
de elementos que posee. Un conjunto es finito si podemos contar la
cantidad de elementos que lo conforman.
Por ejemplo, el conjunto de las letras del idioma
castellano es finito porque en total son letras. En la imagen de la
derecha se muestran otros conjuntos finitos. Te puedes dar cuenta
que los conjuntos unitarios también son finitos.
Conjuntos infinitos
No es fácil encontrar en la naturaleza ejemplos de este
tipo de conjuntos. Los conjuntos infinitos son aquellos a los
cuales no les podemos contar la cantidad de elementos que los componen.
El método más fácil para representar este tipo de conjuntos es por comprensión.
Basta con mencionar las características que tienen en común los elementos del
conjunto y los estaremos determinando a todos. Considera el conjunto de
los números que terminan en tres, podríamos definirlo así: Sea
También existe una manera de representar algunos conjuntos
infinitos por extensión.
Basta exhibir los primeros elementos del conjunto e indicar con puntos
suspensivos que la lista continua indefinidamente. En el caso del conjunto,
definido en el párrafo anterior y conformado por los números que terminan en
tres, se tiene
Los ejemplos más sencillos y comunes de conjuntos infinitos
los encontramos en los números. ¿Cuántos números pares hay? ¿cuántos
múltiplos tiene el tres? Estos conjuntos son infinitos, y no es porque
este más allá de nuestra capacidad contar la cantidad de elementos que
tienen. Es que es imposible hacerlo porque no hay un número que
represente la cantidad de elementos que el conjunto contiene.
Igualdad de conjuntos
Conjunto de personas. El conjunto de «personas»
mostrado en la imagen, A, tiene 8 miembros. Este conjunto puede
representarse mediante llaves o
mediante un diagrama de Venn. El orden de las personas
en A es irrelevante.
Un conjunto está totalmente determinado por sus elementos.
Por ello, la igualdad de conjuntos se establece como:
Propiedad de la extensionalidad
Dos conjuntos A y B que tengan los
mismos elementos son el mismo conjunto, A = B.
Esta propiedad tiene varias consecuencias. Un mismo
conjunto puede especificarse de muchas maneras distintas, en particular
extensivas o intensivas. Por ejemplo, el conjunto A de los números
naturales menores que 5 es el mismo conjunto que A′, el conjunto de los
números 1, 2, 3 y 4. También:
B = {verde, blanco, rojo} = {colores de la bandera de
México}
C = {a, e, i, o, u} = {vocales del español}
D = {Palos de la baraja francesa} = {♠, ♣, ♥, ♦}
El orden en el que se precisan los elementos tampoco se
tiene en cuenta para comparar dos conjuntos:
B = {verde, blanco, rojo} = {rojo, verde, blanco}
C = {a, e, i, o, u} = {e, i, u, a, o}
Además, un conjunto no puede tener elementos «repetidos»,
ya que un objeto solo puede o bien ser un elemento de dicho conjunto o no
serlo. Se da entonces que, por ejemplo:
{1, 2} = {1, 2, 1}
En ausencia de alguna característica adicional que distinga
los «1» repetidos, lo único que puede decirse del conjunto de la derecha es que
«1» es uno de sus elementos.
Conjunto vacío
Conjunto
vacío
El conjunto que no contiene ningún elemento se llama el
conjunto vacío y se denota por o
simplemente {}. Algunas teorías axiomáticas de conjuntos aseguran
que el conjunto vacío existe incluyendo un axioma del conjunto vacío. En otras
teorías, su existencia puede deducirse. Muchas posibles propiedades de
conjuntos son trivialmente válidas para el conjunto vacío.
Propiedades
En la teoría de conjuntos axiomática estándar, por el Axioma de extensionalidad, dos conjuntos son iguales si tienen los mismos elementos; por lo tanto solo puede haber un conjunto sin ningún elemento. Por consiguiente, solo hay un único conjunto vacío, y hablamos de "el conjunto vacío" en lugar de "un conjunto vacío".
Para cualquier conjunto A:
(Ver operaciones con conjuntos)
- El conjunto vacío es un subconjunto de A:
- La unión de A con el conjunto vacío es A:
- La intersección de A con el conjunto vacío es el conjunto vacío:
- El producto cartesiano de A y el conjunto vacío es el conjunto vacío:
El conjunto vacío tiene las siguientes propiedades:
- Su único subconjunto es el propio conjunto vacío:
- El conjunto potencia del conjunto vacío es el conjunto que contiene únicamente el conjunto vacío:
- Su número de elementos (cardinalidad) es cero:
(La lista de símbolos matemáticos empleados se
encuentra aquí).
Subconjuntos
Subconjunto
Subconjunto. B es un subconjunto de A (en
particular un subconjunto propio).
Un subconjunto A de un conjunto B, es un
conjunto que contiene algunos de los elementos de B (o quizá todos):
|
Un conjunto A es un subconjunto del conjunto B si
cada elemento de A es a su vez un elemento de B. |
Cuando A es
un subconjunto de B, se denota como A ⊆ B y se dice que «A está
contenido en B». También puede escribirse B ⊇ A, y decirse que B es
un superconjunto de A y también «B contiene a A»
o «B incluye a A».
Todo conjunto A es un subconjunto de sí mismo, ya
que siempre se cumple que «cada elemento de A es a su vez un elemento
de A». Es habitual establecer una distinción más fina mediante el concepto
de subconjunto propio: A es un subconjunto propio de B si
es un subconjunto de B pero no es igual a B. Se denota
como A ⊊ B,
es decir: A ⊆ B pero A ≠ B (y
equivalentemente, para un superconjunto propio, B ⊋ A).n 2
Ejemplos.
El «conjunto de todos los hombres» es un subconjunto propio
del «conjunto de todas las personas».
{1, 3} ⊊ {1,
2, 3, 4}
{1, 2, 3, 4} ⊆ {1,
2, 3, 4}
Conjuntos disjuntos
Conjuntos disjuntos
Dos conjuntos A y B son disjuntos si no
tienen ningún elemento en común. Por ejemplo, los conjuntos de los números racionales y los números irracionales son disjuntos:
no hay ningún número que sea a la vez racional e irracional. La intersección de dos conjuntos
disjuntos es el conjunto vacío.
Cardinalidad
Número cardinal
Los conjuntos pueden ser finitos o infinitos.
En el caso de un conjunto finito se pueden contar los elementos del conjunto:
|
El número de elementos de un conjunto finito es su cardinal. |
El cardinal se denota
por |A|, card(A) o #A. Así, en los ejemplos anteriores,
se tiene que |A| = 4 (cuatro números), |B| = 3 (tres
colores) y |F| = 10 (diez cuadrados). El único conjunto cuyo cardinal
es 0 es el conjunto vacío ∅.
Existen, a su vez, determinadas propiedades de
cardinalidad. Si tomamos como ejemplo dos conjuntos, A y B:
Y en el caso de tres conjuntos, A, B y C:
En un conjunto infinito no hay un número finito de
elementos. Es el caso por ejemplo de los números naturales: N = {1, 2, 3, …}.
Sin embargo, existe una manera de comparar conjuntos infinitos entre sí, y se
obtiene que existen conjuntos infinitos «más grandes» que otros. El «número de
elementos» de un conjunto infinito es un número transfinito.
Cardinalidad de los
reales
Número real
Uno de los resultados más importantes de Georg Cantor fue
que la cardinalidad de los reales () es más grande que la de
los números naturales ().
Esto es, que hay más números reales R que números enteros N.
Concretamente, Cantor mostró que .
La hipótesis del continuo afirma que no existen conjuntos
con cardinalidades intermedias entre los naturales y
los reales:
- No
existe ningún conjunto A tal que su cardinal |A| cumpla:
Si se asume el axioma de elección, la estructura de los
cardinales infinitos es más clara: todos los cardinales infinitos son álefs y están bien
ordenados, por lo que existe solo un cardinal inmediatamente
superior a ℵ0,
denotado por ℵ1. La
hipótesis es equivalente entonces a:
- El
cardinal del conjunto de los números reales es el inmediatamente superior
al cardinal de los números naturales:
OPERACIONES CON CONJUNTOS
Operaciones con conjuntos
Unión
Intersección
Diferencia
Complemento
Diferencia simétrica
Álgebra de conjuntos
Existen varias operaciones básicas que pueden realizarse,
partiendo de ciertos conjuntos dados, para obtener nuevos conjuntos:
- Unión:
(símbolo ∪)
La unión de dos conjuntos A y B,
que se representa como A ∪ B, es el conjunto de todos los
elementos que pertenecen al menos a uno de los conjuntos A y B.
- Intersección:
(símbolo ∩) La intersección de
dos conjuntos A y B es el conjunto A ∩ B de
los elementos comunes a A y B.
- Diferencia:
(símbolo \) La diferencia del conjunto A con B es
el conjunto A \ B que resulta de eliminar de A cualquier
elemento que esté en B.
- Complemento:
El complemento de
un conjunto A es el conjunto A∁ que contiene
todos los elementos que no pertenecen a A, respecto a un conjunto U que lo contiene.
- Diferencia
simétrica: (símbolo Δ) La diferencia simétrica de dos
conjuntos A y B es el conjunto A Δ B con
todos los elementos que pertenecen, o bien a A, o bien a B, pero
no a ambos a la vez.
- Producto
cartesiano: (símbolo ×) El producto cartesiano de dos
conjuntos A y B es el conjunto A × B de
todos los pares ordenados (a, b) formados
con un primer elemento a perteneciente a A, y un segundo
elemento b perteneciente a B.
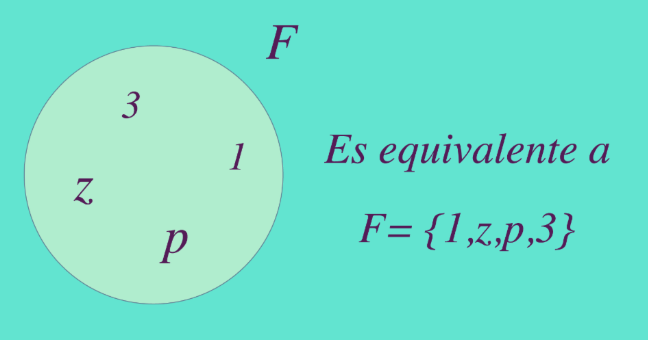












No hay comentarios.:
Publicar un comentario