LOGICA PROPORCIONAL

 

HISTORIA

La lógica proposicional fue finalmente refinada usando la lógica simbólica, se acreditó ser el fundador de la lógica simbólica el matemático Gottfried Leibniz siglo XVII/XVIII, por su trabajo ratiocinator del cálculo. Aunque su trabajo era unos de los primeros, era desconocido para la comunidad lógica más grande. En consecuencia, muchos de los avances logrados por Leibniz fueron recreados por lógicos como George Boole y Augustus De Morgan completamente independientes a Leibniz.

Así como la lógica proposicional puede considerarse un avance de la lógica silogísta anterior, la lógica de predicados de Gottlob Frege era un avance de la lógica proposicional anterior. Un autor describe esta lógica como la combinación de los rasgos distintivos de la lógica silogística y la lógica proposicional. Por lo tanto, la lógica predicativa marcó el comienzo de una nueva era en la historia de la lógica; sin embargo, los avances en la lógica proposicional se hicieron aún después de Frege, incluyendo Deducción Natural, Árboles de la Verdad y Tablas de Verdad. La deducción natural fue inventada por Gerhard Gentzen y Jan Lukasiewicz. Los árboles de la verdad fueron inventados por Evert Willem Beth. La invención de las tablas de la verdad, sin embargo, es de atribución controvertida.

Dentro de las obras de Frege y Bertrand Russell, hay ideas que influyen en la invención de las tablas de la verdad. La estructura tabular real se acredita generalmente a Ludwig Wittgenstein o a Emil Post ( o ambos independientemente). Adeám de Frege y Russell, otros acreditados con ideas anteriores a las tablas de la verdad incluyen a Philo, Boole, Charles Sanders Peirce. Otros acreditados de la estructura tabular incluyen Lukasiewicz, Alfred North Whitehead, Guillermo Stanley Jevons, John Venn, y Clarence Irving Lewis. En última instancia, algunos han llegado a la conclusión, como John Shosky, de que " está lejos de estar claro que a cualquier persona se le debe dar el título de 'inventor' de las tablas de la verdad".

Proposiciones y Conectivos Lógicos

 

En un intento por sistematizar el razonamiento matemático, surge el concepto de Lógica Proposicional. Como su nombre lo explícita, trabajaremos con proposiciones lógicas; las cuales poseen un valor de verdad (verdadero o falso). Por convención, las denotaremos con letras minúsculas. Por ejemplo; p,q,r,s.p,q,r,s.

La lógica es la disciplina que trata de los métodos, modos y formas de| razonamiento humano. Ofrece reglas y técnicas para determinar si un argumento es válido o no. Una de las metas fundamentales de la lógica es eliminar las ambigüedades del lenguaje ordinario. introduciendo símbolos y conectivos lógicos en la construcción de proposiciones.

Definición 

una proposición es toda oración o enunciado respecto de la cual se puede decir si es verdadera o falsa, pero no ambas a la vez. Es decir, toda proposición está asociada a un valor de verdad, la cual puede ser verdadera o bien falsa. Así, si una proposición es verdadera. se dice que su valor de verdad es V y si es falsa, se dice que su valor de verdad es F.

Notación y conectivos lógicos 

En lógica, una conectiva lógica, o también conectiva (también llamado operador o conectores lógicos) es un símbolo o palabra que se utiliza para conectar dos fórmulas bien formadas o sentencias (atómicas o moleculares), de modo que el valor de verada de la fórmula compuesta depende del valor de verdad de las fórmulas componentes

 

operaciones proposicionales 

Así como en aritmética y en álgebra se estudian operaciones entre números, en lógica se estudian operaciones entre proposiciones.

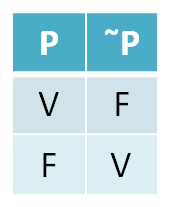
LA NEGACIÓN

La negación de una proposición p se escribe “~ p” y se lee “no p” ó “no es cierto que p” ó “es falso que p” y es otra proposición que niega que se cumpla p.

 

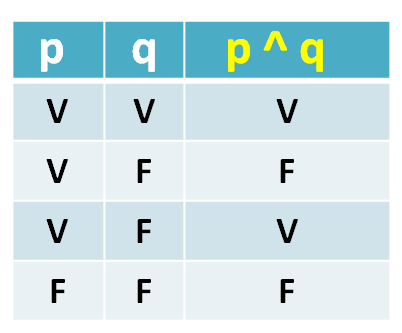
LA CONJUNCIÓN

Dadas las proposiciones p, q, se simboliza “p Ù q” y se lee “p y q”, sólo es verdadero cuando ambos son verdaderos, en los demás casos siempre es falso.

NOTA: En toda proposición, las palabras: “pero”, “sin embargo”, “además”, “no obstante”, “aunque”, “a la vez”, etc. Equivalen al conectivo  ” Ù “

 

 

LA DISYUNCIÓN INCLUSIVA

 

Dadas dos proposiciones p, q se escribe “p Ú q”  y se lee “p ó q”, sólo es falso cuando ambos son falsos, en los demás casos siempre es verdadero.

 

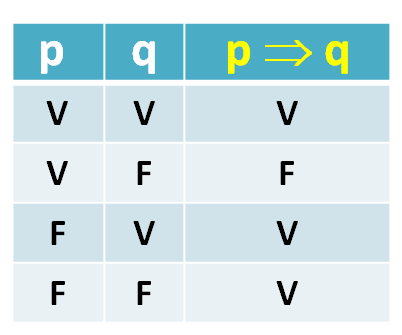
LA CONDICIONAL

Dadas dos proposiciones p, q se escribe “p ® q” y se lee “si p entonces q” ó “p implica q” ó “p es suficiente para que q”, etc., sólo es falso cuando el primero es verdadero y el segundo es falso, en los demás casos siempre es verdadero. ( p = antecedente y q = consecuente)

LA BICONDICIONAL

Dadas dos proposiciones p, q se escribe “p « q” y se lee “p si y solo si q”, es verdadero cuando los valores de verdad son iguales y es falso cuando los dos valores de verdad son diferentes.

 

LA DISYUNCIÓN EXCLUSIVA

Dadas las proposiciones p, q se escribe “p D q” y se lee “o bien p o bien q”, es falso si los valores de verdad de las proposiciones son iguales y es verdadero si los valores de verdad de las proposiciones son diferentes.

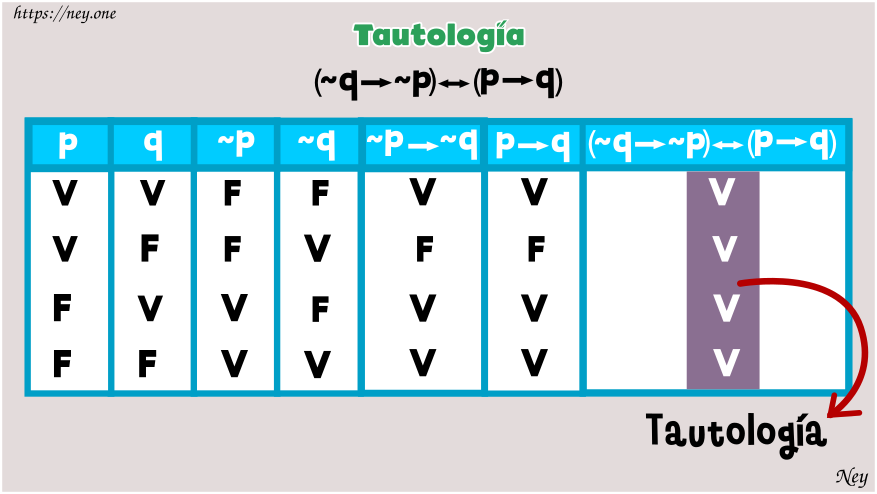
TAUTOLOGÍA

Llamamos tautología si en la columna resultado todos los valores son verdaderos

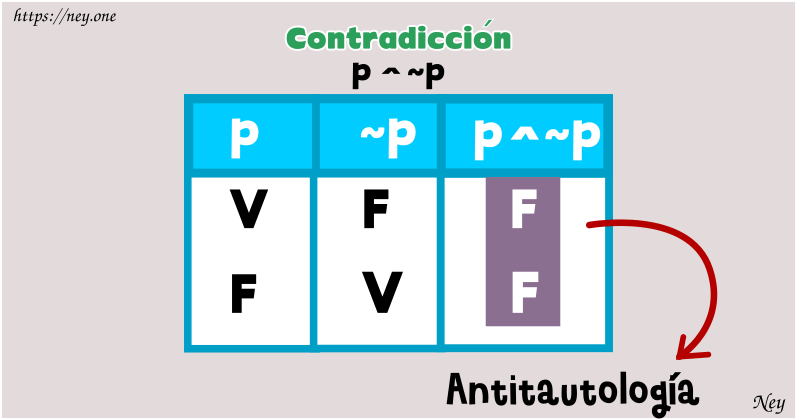
CONTRADICCIÓN

Llamamos contradicción si en la columna resultado todos los valores son falsos.

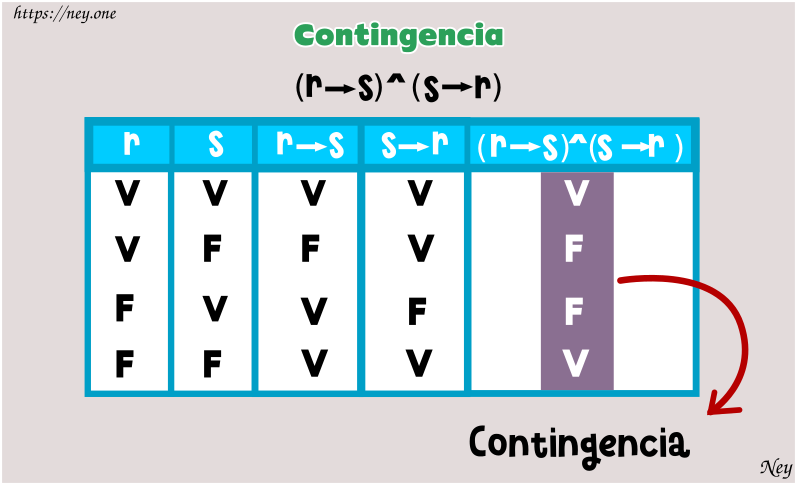
CONTINGENCIA

Llamamos contingencia si en la columna resultado se encuentra verdaderos y falsos, sin considerar cuántos verdaderos o cuántos falsos existan, es suficiente que se encuentren ambos.

IMPLICACIÓN Y EQUIVALENCIA LÓGICAS

IMPLICACIÓN LÓGICA

Se llama implicación lógica o simplemente implicación a toda condicional p ® q que sea tautología. Ejemplo: Verifica si la siguiente condicional es una implicación lógica: [(p ® q) Ù ~ q] ® ~ p

En la columna resultado se observa los valores de verdad, en este caso todos son verdaderos. Entonces, afirmamos que la condicional es tautología, por tanto, es una implicación lógica. Si en la columna resultado se obtiene contradicción o contingencia, entonces, no existe implicación lógica.

EQUIVALENCIA LÓGICA

Se llama equivalencia lógica o simplemente equivalencia a todo bicondicional p « q que sea tautología. Ejemplo: Verifica si el siguiente bicondicional es una equivalencia lógica: [p Ù (p Ú q)] « p

Como se verifica que el resultado de la bicondicional, es tautología, afirmamos que es una equivalencia lógica.

Entonces, podemos afirmar que: [p Ù (p Ú q)] º p

LEYES DEL ÁLGEBRA PROPOSICIONAL

Las proposiciones equivalentes se convierten en leyes lógicas. Existen infinitas proposiciones equivalentes. Pero sólo consideraremos algunas a las que llamaremos leyes del álgebra proposicional

Las leyes del álgebra proposicional se aplican o utilizan en la validación de proposiciones compuestas, es decir, para determinar el valor de verdad de una proposición. Además, se utiliza en la simplificación de proposiciones compuestas.

LA INFERENCIA O ARGUMENTO LÓGICOS

Se llama inferencia lógica o argumento lógico a toda condicional de la forma: (p₁ Ù p₂ Ù … Ù p_k ) ® q donde las proposiciones p1, p2, … pk son llamadas premisas, y originan como consecuencia otra proposición denotada por q llamada conclusión. Una inferencia puede ser tautología, contingencia o contradicción. Si la condicional es una tautología, es decir si es una implicación entonces recibe el nombre de argumento o inferencia válidos. Si la condicional no es una tautología entonces se denomina falacia o simplemente argumento no válido.